Compare genotype and phenotype groups

Fisher exact test (FET)

The Fisher exact test (FET) calculates the exact probability value for the relationship between two dichotomous variables. In our implementation, the two dichotomous variables are the genotype and the phenotype. For instance, the individuals of the cohort may be divided according to whether or not they have a nonsense variant and according to whether or not they have Strabismus (HP:0000486).

The results of FET are expressed in terms of an exact probability (P-value), varying within 0 and 1. Two groups are considered statistically significant if the P-value is less than the chosen significance level (usually \(\alpha = 0.05\)).

The following graphic shows an example contingency table that is used to conduct a Fisher exact test. We are comparing the frequency of strabismus in individuals with missense and nonsense variants:

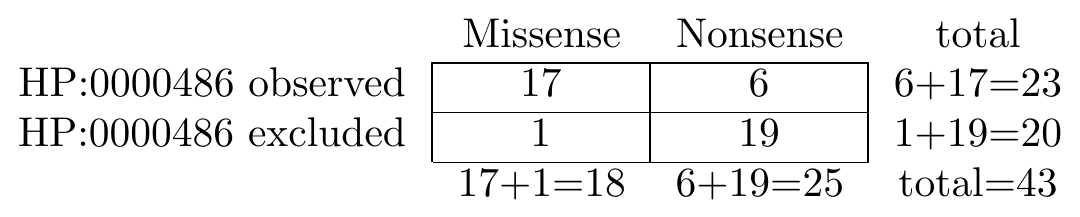
To perform the corresponding test in Python, we would use the following code.

>>> import scipy.stats as stats
>>> contingency_table = [
... #   Missense,    Nonsense
...    [17,          6       ],  # Strabismus observed
...    [1,          19       ],  # Strabismus excluded
... ]
>>> oddsratio, p_value = stats.fisher_exact(contingency_table)
>>> float(oddsratio)
53.833333333333336
>>> float(p_value)
5.432292015291845e-06

The p_value evaluates to 5.432292015291845e-06, meaning there is a significant difference between the groups.

The Fisher exact test evaluates whether the observed frequencies in a contingency table significantly deviate from the frequencies we would expect if there were no association between the variables. We want to test whether the frequency of HP:0000486` is significantly higher or lower in one genotype group compared to what would be expected if there were no association. Note that by default, the two-tailed Fisher exact test is performed, meaning we have no hypothesis as to whether there is a higher or lower frequency in one of the genotype groups.

However, we are typically interested in testing the associations between the genotype and multiple phenotypic features at once. GPSEA takes advantage of the HPO structure and simplifies the testing for all HPO terms encoded in the cohort.

Example analysis

Let’s illustrate this in a real-life example of the analysis of the association between frameshift variants in TBX5 gene and congenital heart defects in the dataset of 156 individuals with mutations in TBX5 whose signs and symptoms were encoded into HPO terms, stored as phenopackets of the GA4GH Phenopacket Schema, and deposited in Phenopacket Store.

Note

The shorter version of the same analysis has been presented in the Tutorial.

Load cohort

For the purpose of this analysis, we will load the Cohort from a JSON file. The cohort was prepared from phenopackets as described in Create a cohort from GA4GH phenopackets section, and then serialized as a JSON file following the instructions in Persist the cohort for later section.

>>> import json
>>> from gpsea.io import GpseaJSONDecoder
>>> fpath_cohort_json = 'docs/cohort-data/TBX5.0.1.20.json'
>>> with open(fpath_cohort_json) as fh:
...     cohort = json.load(fh, cls=GpseaJSONDecoder)
>>> len(cohort)
156

Configure analysis

We want to test the association between frameshift TBX5 variants and phenotypic abnormalities. GPSEA exposes a flexible predicate API that lets us create genotype and phenotype predicates to assign the cohort members into genotype and phenotype categories based on the variants and the HPO terms. We need to create one genotype predicate and one or more phenotype predicates.

Genotype predicate

We want to separate the patients into two groups: a group with a frameshift variant and a group without a frameshift variant (i.e. any other heterozygous variant). We will use the MANE transcript for the analysis:

>>> tx_id = 'NM_181486.4'

Building a genotype predicate is a two step process. First, we create a VariantPredicate to test if the variant is predicted to lead to a frameshift in NM_181486.4:

>>> from gpsea.model import VariantEffect
>>> from gpsea.analysis.predicate.genotype import VariantPredicates
>>> is_frameshift = VariantPredicates.variant_effect(VariantEffect.FRAMESHIFT_VARIANT, tx_id)
>>> is_frameshift.description
'FRAMESHIFT_VARIANT on NM_181486.4'

and then we wrap is_frameshift in a monoallelic_predicate to classify each TBX5 cohort member either as an individual with one frameshift allele (Frameshift) or as an idividual with one non-frameshift allele (Other):

>>> from gpsea.analysis.predicate.genotype import monoallelic_predicate
>>> gt_predicate = monoallelic_predicate(
...     a_predicate=is_frameshift,
...     a_label="Frameshift",
...     b_label="Other",
... )
>>> gt_predicate.group_labels
('Frameshift', 'Other')

In the subsequent analysis, gt_predicate will assign a cohort member into the respective group. Note, any patient with \(0\) or \(\ge 2\) alleles will be omitted from the analysis.

Phenotype predicates

We recommend testing the genotype phenotype association for all HPO terms that annotate the cohort members, while taking advantage of the HPO graph structure and of the True path rule. We will use the prepare_predicates_for_terms_of_interest() utility function to generate phenotype predicates for all HPO terms.

The function needs HPO to prepare predicates, hence we need to load HPO:

>>> import hpotk
>>> store = hpotk.configure_ontology_store()
>>> hpo = store.load_minimal_hpo(release='v2024-07-01')

and then we can create the predicates

>>> from gpsea.analysis.predicate.phenotype import prepare_predicates_for_terms_of_interest
>>> pheno_predicates = prepare_predicates_for_terms_of_interest(
...     cohort=cohort,
...     hpo=hpo,
... )
>>> len(pheno_predicates)
369

The function finds 369 HPO terms that annotate at least one individual, including the indirect annotations whose presence is implied by the True path rule.

Statistical analysis

We will use Fisher exact test (FET) to test the association between genotype and phenotype groups, as described previously.

In the case of this cohort, we can test association between having a frameshift variant and one of 369 HPO terms. However, testing multiple hypotheses on the same dataset increases the risk of finding a significant association solely by chance. GPSEA uses a two-pronged strategy to reduce the number of tests and, therefore, mitigate this risk: a phenotype multiple testing (MT) filter and multiple testing correction (MTC).

Phenotype MT filter selects a (sub)set of HPO terms for testing, for instance only the user-selected terms (see SpecifyTermsStrategy) or the terms selected by HpoMtcFilter.

Multiple testing correction then adjusts the nominal p values for the increased risk of false positive G/P associations. The available MTC procedures are listed in the Multiple-testing correction procedures section.

We must pick one of these to perform genotype-phenotype analysis.

Default analysis

We recommend using HPO MT filter (HpoMtcFilter) as a phenotype MT filter and Benjamini-Hochberg for multiple testing correction. The default analysis can be configured with configure_hpo_term_analysis() convenience method.

>>> from gpsea.analysis.pcats import configure_hpo_term_analysis
>>> analysis = configure_hpo_term_analysis(hpo)

Custom analysis

If the defaults do not work, we can configure the analysis manually. First, we choose a phenotype MT filter (e.g. HpoMtcFilter):

>>> from gpsea.analysis.mtc_filter import HpoMtcFilter
>>> mtc_filter = HpoMtcFilter.default_filter(hpo, term_frequency_threshold=.2)

Note

See the MT filters: Choosing which terms to test section for more info on the available MT filters.

then a statistical test (e.g. Fisher Exact test):

>>> from gpsea.analysis.pcats.stats import FisherExactTest
>>> count_statistic = FisherExactTest()

Note

See the gpsea.analysis.pcats.stats module for the available multiple testing procedures (TL;DR, just Fisher Exact test at this time).

and we finalize the setup by choosing a MTC procedure (e.g. fdr_bh for Benjamini-Hochberg) along with the MTC alpha:

>>> mtc_correction = 'fdr_bh'
>>> mtc_alpha = 0.05

The final HpoTermAnalysis is created as:

>>> from gpsea.analysis.pcats import HpoTermAnalysis
>>> analysis = HpoTermAnalysis(
...     count_statistic=count_statistic,
...     mtc_filter=mtc_filter,
...     mtc_correction='fdr_bh',
...     mtc_alpha=0.05,
... )

Analysis

We can now test associations between the genotype groups and the HPO terms:

>>> result = analysis.compare_genotype_vs_phenotypes(
...     cohort=cohort,
...     gt_predicate=gt_predicate,
...     pheno_predicates=pheno_predicates,
... )
>>> len(result.phenotypes)
369
>>> result.total_tests
24

Thanks to phenotype MT filter, we only tested 24 out of 369 terms. We can learn more by showing the MT filter report:

>>> from gpsea.view import MtcStatsViewer
>>> mtc_viewer = MtcStatsViewer()
>>> mtc_report = mtc_viewer.process(result)
>>> mtc_report  

Phenotype testing report

Phenotype MTC filter: HPO MTC filter

Multiple testing correction: fdr_bh

Performed statistical tests for 24 out of the total of 369 HPO terms.

Using HPO MTC filter, 345 term(s) were omitted from statistical analysis.

Code	Reason	Count
HMF01	Skipping term with maximum frequency that was less than threshold 0.2	10
HMF08	Skipping general term	48
HMF09	Skipping term with maximum annotation frequency that was less than threshold 0.4	287

Genotype phenotype associations

Last, let’s explore the associations. The results include a table with all tested HPO terms ordered by the corrected p value (Benjamini-Hochberg FDR):

>>> from gpsea.view import summarize_hpo_analysis
>>> summary_df = summarize_hpo_analysis(hpo, result)
>>> summary_df  

TBX5 frameshift vs rest

Allele group	Frameshift	Frameshift	Other	Other
	Count	Percent	Count	Percent	Corrected p values	p values
Ventricular septal defect [HP:0001629]	19/19	100%	42/71	59%	0.005806240832840839	0.00024192670136836828
Absent thumb [HP:0009777]	14/31	45%	18/100	18%	0.04456405819223913	0.0037136715160199273
Secundum atrial septal defect [HP:0001684]	4/22	18%	23/55	42%	0.4065940176561687	0.06544319142266644
Triphalangeal thumb [HP:0001199]	13/32	41%	23/99	23%	0.4065940176561687	0.06932119159387057
Muscular ventricular septal defect [HP:0011623]	6/25	24%	8/84	10%	0.4065940176561687	0.08470708701170182
Short thumb [HP:0009778]	8/30	27%	25/69	36%	1.0	0.4870099714553749
Absent radius [HP:0003974]	6/25	24%	9/43	21%	1.0	0.7703831604944444
Atrial septal defect [HP:0001631]	20/20	100%	63/65	97%	1.0	1.0
Abnormal atrial septum morphology [HP:0011994]	20/20	100%	64/64	100%	1.0	1.0
Abnormal cardiac septum morphology [HP:0001671]	28/28	100%	89/89	100%	1.0	1.0
Abnormal cardiac atrium morphology [HP:0005120]	20/20	100%	64/64	100%	1.0	1.0
Hypoplasia of the radius [HP:0002984]	6/14	43%	34/75	45%	1.0	1.0
Abnormal appendicular skeleton morphology [HP:0011844]	34/34	100%	93/93	100%	1.0	1.0
Aplasia/hypoplasia of the extremities [HP:0009815]	22/22	100%	78/78	100%	1.0	1.0
Aplasia/hypoplasia involving the skeleton [HP:0009115]	23/23	100%	80/80	100%	1.0	1.0
Aplasia/hypoplasia involving bones of the upper limbs [HP:0006496]	22/22	100%	78/78	100%	1.0	1.0
Aplasia/hypoplasia involving bones of the extremities [HP:0045060]	22/22	100%	78/78	100%	1.0	1.0
Abnormal long bone morphology [HP:0011314]	13/13	100%	50/50	100%	1.0	1.0
Abnormal hand morphology [HP:0005922]	20/20	100%	75/75	100%	1.0	1.0
Abnormal thumb morphology [HP:0001172]	31/31	100%	58/58	100%	1.0	1.0
Abnormal finger morphology [HP:0001167]	31/31	100%	64/64	100%	1.0	1.0
Abnormal digit morphology [HP:0011297]	33/33	100%	67/67	100%	1.0	1.0
Aplasia/Hypoplasia of fingers [HP:0006265]	19/19	100%	44/44	100%	1.0	1.0
Aplasia/hypoplasia involving bones of the hand [HP:0005927]	19/19	100%	44/44	100%	1.0	1.0

The table shows that several HPO terms are significantly associated with presence of a heterozygous (Frameshift) frameshift variant in TBX5. For example, Ventricular septal defect was observed in 42/71 (59%) patients with no frameshift allele (Other) but it was observed in 19/19 (100%) patients with a frameshift allele (Frameshift). Fisher exact test computed a p value of ~0.000242 and the p value corrected by Benjamini-Hochberg procedure is ~0.005806.